OCR Output Comparison | Datalab (Chandra & Surya)

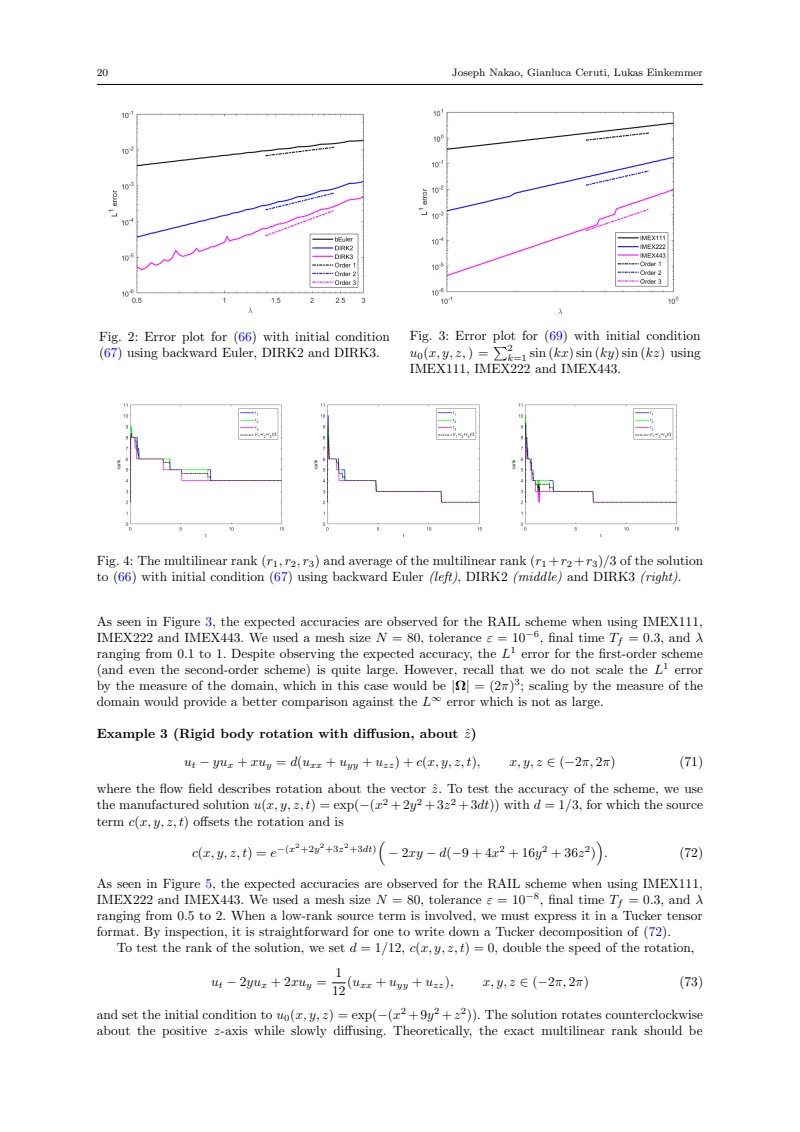
Page 1 of 1

Render HTML

20 Joseph Nakao, Gianluca Ceruti, Lukas Einkemmer

Figure 2 is a log-log plot showing the $L^1$ error versus $\lambda$ for the backward Euler, DIRK2, and DIRK3 schemes. The x-axis ( $\lambda$ ) ranges from 0.5 to 3. The y-axis ( $L^1$ error) ranges from $10^{-6}$ to $10^{-1}$ . The backward Euler scheme (black solid line) shows the highest error, followed by DIRK2 (blue solid line), and DIRK3 (magenta solid line) shows the lowest error. The dashed lines indicate the expected order of convergence: Order 1 (black dashed), Order 2 (blue dashed), and Order 3 (magenta dashed). The DIRK3 scheme closely follows the Order 3 line, indicating third-order convergence.

Fig. 2: Error plot for (66) with initial condition (67) using backward Euler, DIRK2 and DIRK3.

Figure 3 is a log-log plot showing the $L^1$ error versus $\lambda$ for the IMEX111, IMEX222, and IMEX443 schemes. The x-axis ( $\lambda$ ) ranges from $10^{-1}$ to $10^0$ . The y-axis ( $L^1$ error) ranges from $10^{-6}$ to $10^1$ . The IMEX111 scheme (black solid line) shows the highest error, followed by IMEX222 (blue solid line), and IMEX443 (magenta solid line) shows the lowest error. The dashed lines indicate the expected order of convergence: Order 1 (black dashed), Order 2 (blue dashed), and Order 3 (magenta dashed). The IMEX443 scheme closely follows the Order 3 line, indicating third-order convergence.

Fig. 3: Error plot for (69) with initial condition

u_0(x,y,z,)=\sum_{k=1}^2\sin(kx)\sin(ky)\sin(kz)

using IMEX111, IMEX222 and IMEX443.

Figure 4 displays three plots showing the multilinear rank components ( $r_1, r_2, r_3$ ) and the average rank $(r_1+r_2+r_3)/3$ versus time $t$ (from 0 to 15) for the solution to (66) using backward Euler (left), DIRK2 (middle), and DIRK3 (right). The y-axis represents the rank (1 to 11). The plots show that the multilinear rank remains low (around 3 to 4) for all schemes and time steps, indicating efficient low-rank approximation. The average rank is consistently around 3.5 to 4.

Fig. 4: The multilinear rank (

r_1, r_2, r_3

) and average of the multilinear rank (

(r_1+r_2+r_3)/3

) of the solution to (66) with initial condition (67) using backward Euler (left), DIRK2 (middle) and DIRK3 (right).

As seen in Figure 3, the expected accuracies are observed for the RAIL scheme when using IMEX111, IMEX222 and IMEX443. We used a mesh size $N=80$ , tolerance $\varepsilon=10^{-6}$ , final time $T_f=0.3$ , and $\lambda$ ranging from 0.1 to 1. Despite observing the expected accuracy, the $L^1$ error for the first-order scheme (and even the second-order scheme) is quite large. However, recall that we do not scale the $L^1$ error by the measure of the domain, which in this case would be $|\Omega|=(2\pi)^3$ ; scaling by the measure of the domain would provide a better comparison against the $L^\infty$ error which is not as large.

Example 3 (Rigid body rotation with diffusion, about $\hat{z}$ )

$u_t-yu_x+xu_y=d(u_{xx}+u_{yy}+u_{zz})+c(x,y,z,t), \quad x,y,z\in(-2\pi,2\pi) \tag{71}$

where the flow field describes rotation about the vector $\hat{z}$ . To test the accuracy of the scheme, we use the manufactured solution $u(x,y,z,t)=\exp(-(x^2+2y^2+3z^2+3dt))$ with $d=1/3$ , for which the source term $c(x,y,z,t)$ offsets the rotation and is

$c(x,y,z,t)=e^{-(x^2+2y^2+3z^2+3dt)}\left(-2xy-d(-9+4x^2+16y^2+36z^2)\right). \tag{72}$

As seen in Figure 5, the expected accuracies are observed for the RAIL scheme when using IMEX111, IMEX222 and IMEX443. We used a mesh size $N=80$ , tolerance $\varepsilon=10^{-8}$ , final time $T_f=0.3$ , and $\lambda$ ranging from 0.5 to 2. When a low-rank source term is involved, we must express it in a Tucker tensor format. By inspection, it is straightforward for one to write down a Tucker decomposition of (72).

To test the rank of the solution, we set $d=1/12$ , $c(x,y,z,t)=0$ , double the speed of the rotation,

$u_t-2yu_x+2xu_y=\frac{1}{12}(u_{xx}+u_{yy}+u_{zz}), \quad x,y,z\in(-2\pi,2\pi) \tag{73}$

and set the initial condition to $u_0(x,y,z)=\exp(-(x^2+9y^2+z^2))$ . The solution rotates counterclockwise about the positive $z$ -axis while slowly diffusing. Theoretically, the exact multilinear rank should be